匡继昌的不等式著作”常用不等式(Applied Inequalities)”名头很大. 我拥有的第一本是第二版, 由湖南教育出版社出版, 是 \(32\) 开, 不是后来第三版, 第四版的 \(16\) 开. 第二版的页码好像比第三部, 第四版要少那么一点.
当年我阅读这书, 几何不等式这一章, 有这么一个不等式(也就是第四版 \(244\) 页的 \(76\)), 是 Bandila. V. 在 1985 年提出:
\begin{equation}\frac Rr\geqslant\frac bc+\frac cb,\end{equation}
这里 \(R,r\) 分别表示三角形 \(ABC\) 的外接圆半径, 内切圆半径; \(a,b,c\) 为边长.
我当初没有想出证明, 但留下的印象是如此的深刻. 几年过去了, 一些关于三角形的公式对于我, 已然陌生.
设 \(S\) 为 \(\triangle ABC\) 的面积; \(p=\dfrac{a+b+c}2\) 是半周长; \(A,B,C\) 为内角; \(t_a,t_b,t_c\) 为内角平分线长; \(h_a,h_b,h_c\) 为高.
先做一点准备工作.
Lemma 1 \(\dfrac Rr=\dfrac{abc}{4(p-a)(p-b)(p-c)}\).
这结论容易建立. \(S=\dfrac{abc}{4R},S=pr\), 以及 Heron’s formula \(S=\sqrt{p(p-a)(p-b)(p-c)}\) 是熟知的. 经过一点很简单的计算, 可得引理 1.
设 \(x=p-a,y=p-b,z=p-c\), 于是
\[\frac Rr=\frac{(x+y)(y+z)(z+x)}{4xyz}.\]
我们想证明 \((1)\), 只要证明, 当 \(x,y,z\gt0\) 时, 有
\[\frac{(x+y)(y+z)(z+x)}{4xyz}\geqslant\frac{x+z}{x+y}+\dfrac{x+y}{x+z}.\]
也就是说, 指出
\begin{equation}(x+y)^2(y+z)(z+x)^2\geqslant 4xyz[(x+z)^2+(x+y)^2]\end{equation}
即可.
\((x+y)^2z\geqslant4xyz\) 导出
\[z(x+y)^2(z+x)^2\geqslant 4xyz(z+x)^2.\]
同样, 由 \(y(z+x)^2\geqslant4xyz\) 可得
\[y(x+y)^2(z+x)^2\geqslant 4xyz(x+y)^2.\]
我们的目标 \((2)\), 立马呈现在眼前. \(\Box\)
这个证明是传统的. 有更巧妙的途径建立 \((1)\).
为此, 我们需要一个关于内角平分线的不等式.
Lemma 2 \(t_a\leqslant\sqrt{p(p-a)}.\) (“常用不等式”第四版 \(270\) 页)
注意 \(t_a=\dfrac2{b+c}\sqrt{bcp(p-a)}\) 即可.
显然
\[h_b^2+h_c^2\leqslant t_b^2+t_c^2\leqslant p(p-b)+p(p-c)=pa.\]
另一方面,
\[h_b^2+h_c^2=4S^2(\frac1{b^2}+\frac1{c^2})=\frac{abc}R\cdot pr\cdot(\frac1{b^2}+\frac1{c^2})=\frac rR\cdot pa\cdot bc(\frac1{b^2}+\frac1{c^2}).\]
综合两方面, 就得到了 \((1)\). \(\Box\)
需要指出的是, \((1)\) 可以进一步推广成非常普遍的形式.
\(r\leqslant2R\sin\frac A2 (1-\sin\frac A2)\)
顺便, 我们解决掉如下不等式:
\begin{equation}r\leqslant2R\sin\frac A2(1-\sin\frac A2),\end{equation}
仅当 \(b=c\) 时, 等号成立. (“常用不等式”第四版 \(245\) 页)
先把引理 1 改头换面成一个等价形式:
Lemma 1′ \(\dfrac r{4R}=\sin\dfrac A2\sin\dfrac B2\sin\dfrac C2\).
这引理的正确, 由下述事实立马保证:
Lemma 3 \(\sin\dfrac A2=\sqrt{\dfrac{(p-b)(p-c)}{bc}}\).
利用余弦定理和半角公式即可. 事实上, 因为 \(\cos A=\dfrac{b^2+c^2-a^2}{2bc}\), 所以
\[\sin\frac A2=\sqrt{\frac{1-\cos A}2}=\sqrt{\frac{a^2-(b-c)^2}{4bc}}=\sqrt{\dfrac{(p-b)(p-c)}{bc}}.\]
于是, 要说明 \((3)\), 只要验证 \(2\sin\dfrac B2\sin\dfrac C2\leqslant1-\sin\dfrac A2\).
这真是再容易不过了: 积化和差. 事实上,
\[2\sin\frac B2\sin\frac C2=\cos\frac{B-C}2-\cos\frac{B+C}2\leqslant1-\sin\frac A2. \Box\]
比外接圆更大的圆
现在考虑 Euler’s inequality 另一种形式的推广. 下面的 \((4)\) 和 \((5)\) 是 Federico Ardila 的工作.
把三角形 \(ABC\) 放进一个更大的圆 \(\omega\): \(A,B,C\) 三点在这圆内或圆周上. 设圆 \(\omega\) 的半径是 \(R^\prime\). 那么
\begin{equation}R^\prime\geqslant2r. \end{equation}
这结果显然可以导出 Euler’s inequality, 而不是相反: \(\triangle ABC\) 是钝角三角形的时候, \(R^\prime\lt R\) 是可能的.
设 \(\omega\) 的中心是 \(O\). 显然, \(3R^\prime\geqslant OA+OB+OC\). 因此, 只要证明 \(OA+OB+OC\geqslant 6r\).
设 \(O\) 关于 \(BC,CA,AB\) 的对称点分别是 \(D,E,F\).
如果 \(O\) 在 \(\triangle ABC\) 内或边上, 那么, 六边形 \(AFBDCE\) 的周长是 \(2(OA+OB+OC)\), 面积是 \(2S\). 根据等周不等式, 周长相等的六边形, 以正六边形的面积最大. 于是 \(\dfrac{\sqrt3\left(OA+OB+OC\right)^2}6\geqslant2S\).
同样的道理, 周长相等的三角形中以正三角形的面积为最大, 因此, \(S\leqslant\dfrac{\sqrt3p^2}9\). 结合 \(S=pr\), 给出 \(p\geqslant3\sqrt3r\). 故 \(S=pr\geqslant3\sqrt3r^2\).
综合两方面, 得到我们的目标 \(OA+OB+OC\geqslant 6r\).
如果 \(O\) 在 \(\triangle ABC\) 外, 且 \(O,A\) 在 \(BC\) 异侧. 这时, 六边形 \(AFBOCE\) 的周长是 \(2(OA+OB+OC)\), 面积 \(\gt2S\). 同上面一样的道理, 可以完成证明. 如果 \(O\) 在射线 \(BA\) 与 \(CA\) 所形成的区域(即 \(A\) 在 \(\triangle OBC\) 内), 那么, 四边形 \(OBDC\) 的周长 \(\lt2(OA+OB+OC)\), 面积 \(\gt2S\). 把这四边形视为退化的六边形, 同上一样可以完成证明. \(\Box\)
外接椭圆
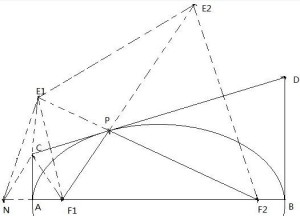
我们继续往前走. 考虑经过 \(\triangle ABC\) 三顶点的椭圆. 假设这椭圆的两个焦点是 \(F_1,F_2\), 椭圆上任意一点到两个焦点的距离之和是常数 \(l\). 我们希望建立
\begin{equation}l\geqslant4r.\end{equation}
记 \(\omega_1\) 是以 \(A\) 为心, \(F_1A\) 为半径的圆. 类似地, 也有圆 \(\omega_2,\omega_3\). 延长 \(F_1A\) 交 \(\omega_1\) 于 \(A_1\). 同样定义 \(B_1,C_1\). 把以 \(F_2\) 为心, \(l\) 为半径的圆记为 \(\omega\). 于是, \(\triangle A_1B_1C_1\) 与 \(\triangle ABC\) 是位似图形, 位似中心是点 \(F_1\), 位似比为 \(2\), 所以 \(\triangle A_1B_1C_1\) 的内切圆半径是 \(2r\).
注意
\[F_2A_1\leqslant F_2A+AA_1=F_2A+F_1A=l,\]
故 \(A_1\) 在 \(\omega\) 内或圆周上. 对于 \(B_1,C_1\) 而言, 同样也是如此. (实际上, \(\omega_1,\omega_2\) 和 \(\omega_3\) 都与 \(\omega\) 内切.) 根据 \((4)\), 得 \(l\geqslant4r\). \(\Box\)
References
- Federico Ardila, A generalization of Euler’s \(R\geqslant2r\).