Geometric construction with the compass alone

 expository, geometry  No Responses »
Jul 222012
 

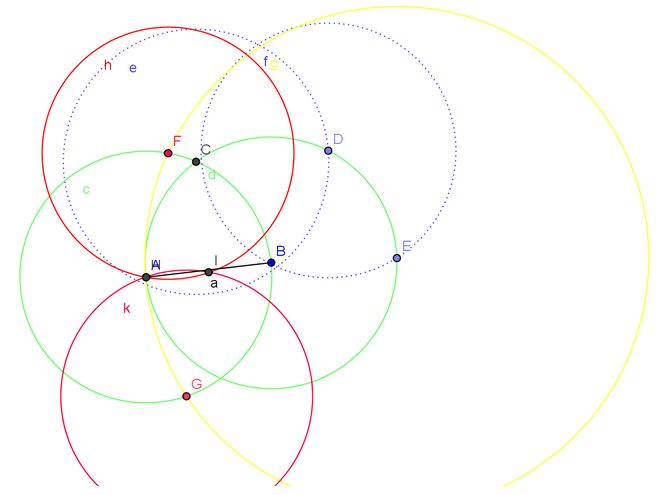
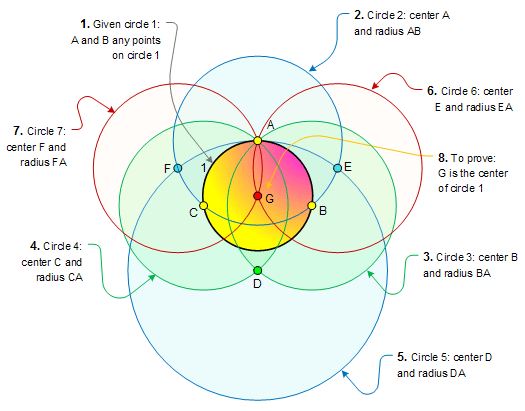
意大利几何学家 L. Mascherom 于 \(1797\) 年证明了, 凡是能用尺规作出的几何图形都可以仅仅使用圆规来完成. \(1833\) 年, Jakob Steiner 根据 Poncelet 的想法, 指出: 如果给定一个圆和它的中心, 那么, 能用尺规作出的几何图形都能单独用直尺来作出.

我一直很好奇, 这些结论究竟是如何证明的? Ross Honsberger 在他的书, “Ingenuity in Mathematics”, 的第 \(15\) 节提供了一个详尽的证明, 这一节的标题是: Mascheroni and Steiner. \(1994\) 年, Norbert Hungerbuhler 给出了 Mascherom 的结果, 所谓的Mohr–Mascheroni定理, 的一个简单的证明.

Find the midpoint of a segment with compass alone

 geometry  No Responses »
Jul 082012
 

仅用圆规找中点

线段 \(AB\) 已给, 仅仅用圆规找其中点.

本题也很有意思, 尺规作图.  不过, 这不算神奇, 即便生锈圆规出马, 也就是把圆的半径固定, 例如 \(1\), 也一样可以完成任务.

作法 

find the midpoint of a segment with compass alone

  1. 分别以 \(A,B\) 为圆心, \(AB\) 为半径画圆(绿色)交于 \(C\);
  2. 在圆 \(B\) 上取 \(D,E\) 两点, 使 \(CD=DE=AB\), 则 \(AE=2AB\);
  3. 以 \(E\) 为圆心,  \(AE\) 为半径画圆(黄色)交圆 \(A\) 于  \(F,G\);
  4. 分別以 \(F,G\) 为圆心, \(AF\) 为半径画圆(红色), 交于 \(A,I\) 两点, 则 \(I\) 就是 \(AB\) 中点.

Find the center of a circle with compass alone

 geometry  No Responses »
Jul 072012
 

仅用圆规找圆心

俺对尺规作图(Compass and straightedge constructions)一直有浓厚的兴趣. 这里有一个有趣的问题:

圆 \(\color{red}O\) 给定, 仅仅使用圆规找出圆心.

下面给出两种作图办法, 没有证明, 但不困难. 图来自网络, 但作图办法不是.

作法 \(1\)

  1. 在圆 \(O\) 上任取一点 \(A\),以 \(A\) 为圆心画圆, 交圆 \(O\) 于 \(B,C\) 兩点;
  2. 分別以 \(B,C\) 为心,\(AB\) 为半径画圆交于 \(D\) 点;
  3. 以 \(D\) 为圆心, \(AD\) 为半径画圆交圆 \(A\) 于 \(E,F\) 两点;
  4. 再分别以 \(E,F\) 为圆心,\(AE\) 为半径画圆,交于 \(A,G\), 则 \(G\) 就是 \(O\) 点.find the center of a circle with compass alone

作法 \(2\)

  1. 在已知圆周上任取一点 \(A\), 以 \(A\) 为圆心, 适当长为半径作圆 \(A\), 交已知圆于两点 \(B,C\);
  2. 从 \(B\) 点出发, 以 \(AB\) 长为半径, 在圆 \(A\) 上连续截取 \(3\) 次得到点 \(D\);
  3. 分别以 \(A,D\) 为圆心,\(CD\) 为半径作弧, 两弧交于 \(E\);
  4. 再以 \(E\) 为圆心, \(EA\) 为半径作弧交圆 \(A\) 于 \(F\);
  5. 分别以 \(A,B\) 为圆心, \(FB\) 为半径作弧, 两弧的交点就是所求已知圆的圆心.