2013 第 29 届中国数学奥林匹克解答
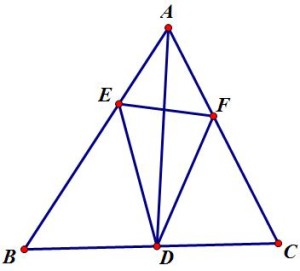
1. \(B\), \(C\), \(F\), \(E\) 四点共圆导出 \(\angle AFE=\angle ABC\), \(\angle AEF=\angle ACB\), 以及 \(AF\gt AE\).
记 \(\triangle ABC\) 的内心为 \(I\), 当然 \(I\) 落在线段 \(AD\) 上; 设 \(\triangle ABC\) 的内切圆切 \(BC\), \(CA\) 与 \(AB\) 分别于点 \(X\), \(Y\), \(Z\), 由 \(AB\gt AC\) 可得 \(X\) 在线段 \(CD\) 上.
因 \(AE\lt AF\lt AB\), 故点 \(E\), \(F\) 关于直线 \(AD\) 的对称点 \(U\), \(V\) 分别在线段 \(AF\), \(BE\)上, 并且 \(\triangle IEV\cong\triangle IUF\).
必要性 如果 \(I\) 是 \(\triangle DEF\) 的外心, 则 \(IE=IF\). 进而, \(\triangle IEV\) 和 \(\triangle IUF\) 都是等腰三角形, \(Y\), \(Z\) 分别是 \(FU\), \(EV\) 的中点. 于是
\[EZ=FY.\]
注意
\begin{equation}BZ=BX, CY=CX,\end{equation}
因之
\[BE+CF=(BZ+ZE)+(CY-FY)=BZ+CY=BX+CX=BC.\]

solution to CMO 2014 Problem 1
充分性 直线 \(AB\), \(AC\) 关于 \(AI\) 对称, \(AZ=AY\), 因此当点 \(Z\) 在线段 \(BV(VE, EA)\) 上时, 点 \(Y\) 必定相应的落在线段 \(CF(FU, UA)\) 上.
如果 \(BE+CF=BC\), 注意 \((1)\) 以及 \(AZ=AY\), 因此点 \(Z\) 必定在线段 \(VE\) 上, 点 \(Y\) 在线段 \(FU\) 上. 由 \(BE+CF=BC\) 可得
\[(BZ+ZE)+(CY-FY)=BZ+CY.\]
因此 \(EZ=FY\). 结合 \(VZ=FY\) 得出 \(EZ=VZ\). 现在我们清楚 \(\triangle IEV\) 是等腰三角形, \(IE=IV\). 对称地, \(\triangle IUF\) 亦是等腰三角形, \(IF=IU\). 顺理成章的, \(IE=IF\). 此外, 从
\[\angle IFA+\angle IEA=\angle IFA+(180^\circ-\angle IEV)=180^\circ\]
得出 \(I\), \(F\), \(A\), \(E\) 四点共圆. \(\angle AIE=\angle AFE=\angle ABD\) 给出 \(B\), \(D\), \(I\), \(E\) 四点共圆. 由 \(\angle IBD=\angle IBE\) 定出 \(ID=IE\). 至此, \(ID=IE=IF\) 表明 \(I\) 即为 \(\triangle DEF\) 的外心.
2. 说穿了, 本题就是要找两个不同的正整数 \(s\), \(t\), 使得不定方程
\begin{equation}x(x+s)=y(y+t) \end{equation}
至少有 \(k\) 组不同的正整数解.
就这个题目而言, 只要定出一对如此的 \(s\), \(t\) 即可. \(s\), \(t\) 的不同选择给出本题不同的解答.
答案 1 令 \(s=2\cdot3^k\), \(t=3^k\), 则
\[x_i=\frac{3^{k-i}(3^{i+1}-1)(3^i-1)}4, y_i=\frac{3^{k-i}(3^{i+1}+1)(3^i-1)}4\]
是方程 \((2)\) 的正整数解, \(i=1\), \(2\), \(\dotsc\), \(k\).
事实上, 注意
\[2x_i+2y_i+s+t=3^{k+1+i}, 2x_i-2y_i+s-t=3^{k-i},\]
以及
\[s+t=3^{k+1}, s-t=3^k,\]
我们可以得出
\[(2x_i+2y_i+s+t)(2x_i-2y_i+s-t)=(s+t)(s-t),\]
这就是 \((2x_i+s)^2-(2y_i+t)^2=s^2-t^2\), 即 \(x_i(x_i+s)=y_i(y_i+t)\), \(i=1\), \(2\), \(\dotsc\), \(k\).
此外, 若 \(1\leqslant i\lt j\leqslant k\), 则
\[3^{i+1}\lt3^{j+1}, 3^k-3^{k-i}\lt3^k-3^{k-j}.\]
结合
\[x_i=\frac{(3^{i+1}-1)(3^k-3^{k-i})}4, y_i=\frac{(3^{i+1}+1)(3^k-3^{k-i})}4,\]
可得出这 \(k\) 个解互不相同.
令
\[n_i=x_i(x_i+s)=y_i(y_i+t), i=1, 2, \dotsc, k,\]
则 \(3^k\), \(2\cdot3^k\in D(n_1)\cap D(n_2)\cap\dotsb\cap D(n_k)\).
答案 2 记 \(p_i=2(k+1-i)\), \(q_i=\dfrac{(2k+2)!!}{p_i}\), 则
\[p_iq_i=(2k+2)!!, q_i\gt p_i, i=0, 1, 2, \dotsc, k.\]
令 \(a_i=\dfrac{q_i+ p_i}2\), \(b_i=\dfrac{q_i- p_i}2\), 则 \(a_i\gt b_i\), \(a_i^2-b_i^2=p_iq_i\), \(i=0\), \(1\), \(2\), \(\dotsc\), \(k\). 此时 \(a_0\), \(a_1\), \(a_2\), \(\dotsc\), \(a_k\); \(b_0\), \(b_1\), \(b_2\), \(\dotsc\), \(b_k\) 都是正整数, 并且
\[a_0^2-b_0^2=a_1^2-b_1^2=a_2^2-b_2^2=\dotsb=a_k^2-b_k^2=(2k+2)!!.\]
此外, 注意
\begin{equation}a_0\lt a_1\lt a_2\lt\dotsb\lt a_k, b_0\lt b_1\lt b_2\lt\dotsb\lt b_k.\end{equation}
然后, 由 \(a_i^2-b_i^2=a_0^2-b_0^2\) 可得
\begin{equation}(a_i+a_0)(a_i-a_0)=(b_i+b_0)(b_i-b_0).\end{equation}
把这个乘积记为 \(n_i\), 即 \(n_i=(a_i+a_0)(a_i-a_0)=(b_i+b_0)(b_i-b_0)\). \((3)\) 表明 \(n_i\) 是正整数, \(i=1\), \(2\), \(\dotsc\), \(k\); \((4)\) 说明 \(D(n_1)\cap D(n_2)\cap\dotsb\cap D(n_k)\) 至少有 \(2\) 个元素 \(2a_0\), \(2b_0\).
3. 先来证明: \(f\) 唯一确定, 并且对于任意正整数 \(n\), 有 \(\dfrac n2\leqslant f(n)\leqslant n\).
对 \(n\) 进行归纳.
当 \(n=1\), \(2\) 时, \(f(n)\) 有唯一确定的取值, 并且适合 \(1\leqslant f(n)\leqslant n\).
假定当 \(n=1\), \(2\), \(\dotsc\), \(k\) 时, \(f(n)\) 都是唯一确定的, 并且适合 \(\dfrac n2\leqslant f(n)\leqslant n\)(\(k\geqslant2\)). 现在我们来考察 \(f(k+1)\).
根据归纳假设, \(1\leqslant f(k)\leqslant k\), 且 \(f(k)\), 更有 \( k+1-f(k)\) 唯一. 由
\[1\leqslant k+1-f(k)\leqslant k\]
唯一定出 \(f(k+1-f(k))\), 且 \(1\leqslant f(k+1-f(k))\leqslant k+1-f(k)\). 进而
\[f(k+1)=f(f(k))+f(k+1-f(k))\]
唯一确定 \(f(k+1)\); 同时
\[f(k+1)=f(f(k))+f(k+1-f(k))\leqslant f(k)+(k+1-f(k))=k+1\]
与
\[f(k+1)=f(f(k))+f(k+1-f(k))\geqslant \frac{f(k)}2+\frac{k+1-f(k)}2=\frac{k+1}2\]
为真.
至此, 我们确信符合要求的函数是唯一存在的.
下一步的目标是达成:
\begin{equation}f(n)+1\geqslant f(n+1)\geqslant f(n), \forall n\in\Bbb N^*.\end{equation}
归纳法确实难以让人喜爱, 何况在同一个问题使用几次.
对 \(n\) 使用数学归纳法.
奠基显然.
假定当 \(n=1\), \(2\), \(\dotsc\), \(k\) 时 (\(k\in\Bbb N^*\)), \(f(n)+1\geqslant f(n+1)\geqslant f(n)\). 我们来观察 \(f(k+2)-f(k+1)\).
显而易见
\begin{equation}\begin{split}&f(k+2)-f(k+1)\\=&(f(f(k+1))+f(k+2-f(k+1)))-(f(f(k))+f(k+1-f(k)))\\=&(f(f(k+1))-f(f(k)))+(f(k+2-f(k+1))-f(k+1-f(k))).\end{split}\end{equation}
这个时候, 朕想起了 1996 年第 37 届 IMO 的第 6 题: 两道题的解答确有某些相似的地方! 朕也想起了”离散”形式的介值定理!
各位看官, 睁大眼睛仔细观看 \((6)\) 的最后一行:
\[\big(f(k+1)-f(k)\big)+\Big(\big(k+2-f(k+1)\big)-\big(k+1-f(k)\big)\Big)=1\]
说明 \(f(k+1)-f(k)\), \(k+2-f(k+1)-(k+1-f(k))\) 有一个 \(0\), 一个 \(1\). 这个事实导致 \(f(f(k+1))-f(f(k))\), \(f(k+2-f(k+1))-f(k+1-f(k))\) 都只能是 \(0\) 或 \(1\), 并且必定有 \(0\). 由此, 我们可以得知, \(f(k+2)-f(k+1)\) 亦仅可能是 \(0\) 或 \(1\).
至此, \((5)\) 的证明完成.
最后来指出: \(f(2^m)=2^{m-1}\), \(m\in\Bbb N^*\).
仍然是归纳法: 对 \(m\) 进行归纳.
由 \(f(1)=f(2)=1\) 得
\[f(3)=f(f(2))+f(3-f(2))=f(1)+f(2)=1+1=2.\]
继续
\[f(4)=f(f(3))+f(4-f(3))=f(2)+f(2)=1+1=2.\]
这表明, 当 \(m=1\), \(2\) 时, \(f(2^m)=2^{m-1}\) 为真.
假设当 \(m=k\) 时 (\(k\geqslant2\)), 成立 \(f(2^m)=2^{m-1}\). 我们希望定出 \(f(2^{k+1})=2^k\).
\(f(n)\geqslant\dfrac n2\) 结合 \((5)\) 表明: 函数 \(f\) 可以取到每个正整数.
这里用到了”离散”形式的介值定理! 此亦是与第 37 届 IMO 的题 6 的一个共同点.
由
\[f\left(2^{k+1}-1\right)\geqslant\frac{2^{k+1}-1}2\]
得 \(f(2^{k+1}-1)\geqslant2^k\). 于是, 存在正整数 \(t\leqslant2^{k+1}-1\), 使得 \(f(t)=2^k\). 然后, \(2f(t)=2^{k+1}\geqslant t+1\) 给出
\[f(t)\geqslant t+1-f(t).\]
据归纳假设, 得
\[ 2^k= f(t)\leqslant f(t+1)=f\big(f(t)\big)+f\big(t+1-f(t)\big)\leqslant 2f\big(f(t)\big)=2f(2^k)=2^k.\]
于是, 可有 \(f(t+1)=2^k\).
如果 \(t+1=2^{k+1}\), 目标已经拿下; 若不然, 同样的道理, 得 \(f(t+2)=2^k\). 如果 \(t+2=2^{k+1}\), \(f(2^{k+1})=2^k\) 梦想成真; 否则, 继续这样重复. 同样的做法经过 \(2^{k+1}-t\) 次后, 可以断定 \(f(2^{k+1})=2^k\). 这完成了归纳证明.
4. \(\omega(n)\) 和 \(\Omega(n)\) 是用来计量 \(n\) 的素因子的个数, 在数论较为重要. 不过它们在初等数论只是打酱油, 现身的次数屈指可数.
先列举 \(\omega(n)\) 和 \(\Omega(n)\) 的几条简单的性质:
引理 1 \(m\), \(n\) 都是正整数, 则
- \(\omega(m)\leqslant\Omega(m)\);
- \(\omega(m)\leqslant\omega(mn)\leqslant\omega(m)+\omega(n)\);
- \(\omega(m^n)=\omega(m)\);
- \(\Omega(mn)=\Omega(m)+\Omega(n)\). 特别, \(\Omega(m^n)=n \Omega(m)\).
下面两个引理分别参见数学奥林匹克命题人讲座”初等数论”(冯志刚, 上海科技教育出版社, 2009) 1.5 节例 7 和 3.1 节例 3. 其中, 引理 2 是改进的一般形式, 引理 3 直接完全照搬. 引理 3 亦可在 “高中竞赛数学教程”(熊斌, 刘诗雄, 武汉大学出版社, 2003, 第二版)第一卷下册 114 页找到(第 8 章-内容同第一版的第 9 章. 修订的时候, 把第 7 章挪动成了第 10 章, 把第 8, 9 , 10 章都前移一章- B 部分的 8-2 节”指数及其应用”是新版才有, 所以第一版无此例题). 难怪, “高中竞赛数学教程”这一章的执笔者也是冯志刚.
引理 2 若 \(m\), \(n\) 都是正奇数, \(a\), \(b\) 是两个互质的正整数, 则 \((a^m+b^m, a^n+b^n)=a^{(m, n)}+b^{(m, n)}\).
引理 3 设 \(a\), \(n\) 都是正整数, 且 \(a\gt1\), 而 \(q\) 是 \(a^{2^n}+1\) 的奇质因子, 则 \(q\equiv1\pmod{2^{n+1}}\).
这几个引理都需要记住: 引理 1 虽然简单, 但简单的道理往往有奇效, 好用的定理也都是”简单”的; 引理 2 的奇特在于那个加号”\(+\)”, 非常有用; 引理 3 是关于质因子的性质的, 本题用来估计质因子的大小.
这三个引理, 尤其后两个, 是本题的关键. 有了它们, 作答本题, 就畅通无阻, 不费任何力了. 注意, 引理 2 我们实际只需要 \(b=1\) 此种特殊情形.
考察 \(k2^{2^np_1p_2\dotsm p_m}\), 其中 \(n\), \(m\) 是正整数, 而 \(p_1\), \(p_2\), \(\dotsc\), \(p_m\) 都是大于 \(1\), 并且两两互质的正奇数. 注意,
\[\dfrac{2^{2^np_1}+1}{2^{2^n}+1}, \dfrac{2^{2^np_2}+1}{2^{2^n}+1}, \dotsc, \dfrac{2^{2^np_m}+1}{2^{2^n}+1}\]
显然都是 \(2^{2^np_1p_2\dotsm p_m}+1\) 的约数. 根据引理 2, 这 \(m\) 个因子两两互质. 因此
\[\omega\left(2^{2^np_1p_2\dotsm p_m}+1\right)\geqslant m.\]
结合引理 1, 有
\begin{equation}\frac{\omega(k2^{2^np_1p_2\dotsm p_m}+k)}{\omega(k2^{2^np_1p_2\dotsm p_m})}\geqslant\frac{\omega(2^{2^np_1p_2\dotsm p_m}+1)}{\omega(k)+1}\geqslant\frac{m}{\omega(k)+1}.\end{equation}
依引理 3, \(2^{2^np_1p_2\dotsm p_m}+1\) 的质因子都大于 \(2^{n+1}\). 于是, 我们可得
\[\Omega\left(2^{2^np_1p_2\dotsm p_m}+1\right)\leqslant\frac{2^np_1p_2\dotsm p_m}{n+1}.\]
因此, 由引理 1,
\begin{equation}\frac{\Omega(k2^{2^np_1p_2\dotsm p_m}+k)}{\Omega(k2^{2^np_1p_2\dotsm p_m})}\leqslant\frac{\Omega(k)+\Omega(2^{2^np_1p_2\dotsm p_m}+1)}{2^np_1p_2\dotsm p_m}\lt\frac{\Omega(k)}{2^n}+\frac1{n+1}.\end{equation}
只要 \(m\), \(n\) 足够大, 由 \((7)\), \((8)\) 可以清楚的看到我们的理想已经成为现实展现在眼前.
引理 2 的证明 冯志刚已经在他的书中写出了证明. 我们这里不抄他的办法, 转而采纳余红兵在他的”数论”一书给出的思路. 余红兵的”数论”有至少三个版本: 这书最早是由中国少年儿童出版社于 1992 年出版, 书名叫做”数学竞赛中的数论问题”; 华东师范大学出版社推出的数学奥林匹克小丛书高中版-就是常说的”小蓝皮”-把这书收入; 大概两年前, 小蓝皮出这书的修订版的时候, 启用了很简明扼要的书名: 数论!
下面是引理 2 的详细论证, 写法与余红兵有所出入: 这里采用同余! \((a^m-1, a^n-1)=a^{(m, n)}-1\) 在他的书, 是第二章”最大公约数与最小公倍数”的例题. 同余的概念要到第六章才姗姗来迟.
记 \(d=(m, n)\). 有正整数 \(u\), \(v\), 使得 \(mu-nv=d\). 设 \(D=(a^m+b^m, a^n+b^n)\). 只要指出 \(D\mid (a^d+b^d)\) 即可.
因 \(a^m\equiv-b^m\pmod D\), 故 \(a^{mu}\equiv (-1)^ub^{mu}\pmod D\), 即
\[a^{nv+d}\equiv (-1)^ub^{nv+d}\pmod D.\]
类似的, 从 \(a^n\equiv-b^n\pmod D\), 得
\[a^{nv}\equiv (-1)^vb^{nv}\pmod D.\]
鉴于 \((a, D)=(b, D)=1\), 于是
\[a^d\equiv (-1)^{u+v}b^d\pmod D.\]
注意 \(u\), \(v\) 的奇偶性相反, 因之 \(a^d+b^d\equiv0\pmod D\).
为了不致误解, 先厘清符号 \(\delta_m(a)\):
定义 4 设 \(m\) 是正整数, \(a\in\Bbb Z\), 且 \((a, m)=1\), 称使得同余式
\[a^r\equiv1\pmod m\]
成立的最小正整数 \(r\), 用 \(\delta_m(a)\) 表之, 为 \(a\) 对模 \(m\) 的阶(也常称为\(a\) 对模 \(m\) 的指数).
引理 3 的证明 这个论证直接摘自冯志刚的书. 由 \(a^{2^n}\equiv-1\pmod q\) 知
\[a^{2^{n+1}}\equiv1\pmod q.\]
于是 \(\delta_q(a)\nmid2^n\), 但 \(\delta_q(a)\mid2^{n+1}\). 这表明 \(\delta_q(a)=2^{n+1}\).
另一方面, 由 Fermat 小定理, \(a^{q-1}\equiv1\pmod q\), 故 \(2^{n+1}\mid (q-1)\), 此即
\[q\equiv1\pmod{2^{n+1}}.\]
我们可以稍微变通下, 考察 \(k2^{p_1p_2\dotsm p_m}\), 其中 \(m\) 是正整数, 而 \(p_1\), \(p_2\), \(\dotsc\), \(p_m\) 是大于 \(3\) 且两两不同的质数. 现在必须这样要求, 这是与前面不一样的地方.
定义 5 对整数 \(n\gt1\), 设 \(q\) 是质数, 且 \(q^s\parallel n\), 其中 \(s\) 是非负整数, 定义
\[v_q(n)=s.\]
对于 \(2^{p_1p_2\dotsm p_m}+1\) 的质因子, 我们有如下事实:
引理 6 记 \(p=\min\{p_1, p_2, \dotsc, p_m\}\). 设质数 \(q\), 使得 \(q\mid (2^{p_1p_2\dotsm p_m}+1)\), 那么
- 若 \(q=3\), 则 \(v_3(2^{p_1p_2\dotsm p_m}+1)=1\) ;
- 若 \(q\gt3\), 则 \(q\geqslant p\).
事实上, 当 \(q=3\) 时, 由引理 2, 得 \((2^{p_1p_2\dotsm p_m}+1, 2^3+1)=3\). 于是 \(3\parallel (2^{p_1p_2\dotsm p_m}+1)\).
若 \(q\gt3\), 仿照引理 3 的证明进行即得:
如果 \(q\lt p\), 由 \(2^{p_1p_2\dotsm p_m}\equiv-1\pmod q\) 知
\[2^{2p_1p_2\dotsm p_m}\equiv1\pmod q.\]
另一方面, 由 Fermat 小定理, \(2^{q-1}\equiv1\pmod q\), 故 \(\delta_q(2)\mid(2p_1p_2\dotsm p_m, q-1)\), 此即
\[\delta_q(2)\mid2.\]
因此, \(q=3\). 这与我们的假定是矛盾的.
至此, 我们也能很容易的解决第 4 题了:
\[\Omega\left(2^{p_1p_2\dotsm p_m}+1\right)\leqslant1+p_1p_2\dotsm p_m\log_p2.\]
类似 \((8)\), 可得
\begin{equation}\frac{\Omega(k2^{p_1p_2\dotsm p_m}+k)}{\Omega(k2^{p_1p_2\dotsm p_m})}\leqslant\frac{\Omega(k)+\Omega(2^{p_1p_2\dotsm p_m}+1)}{p_1p_2\dotsm p_m}\leqslant\frac{\Omega(k)+1}{p^m}+\log_p2.\end{equation}
也可以有另外改变, 来考虑这个问题.
设 \(p\) 是奇质数, \(p_1\), \(p_2\), \(\dotsc\), \(p_m\) 是大于 \(p\) 且两两不同的质数. 我们来考察 \((p-1)^{pp_1p_2\dotsm p_m}+1\), 或者 \((p-1)^{p_1p_2\dotsm p_m}+1\).
引理 7 \((p-1)^{pp_1p_2\dotsm p_m}+1\) 的最小质因子是 \(p\).
其实这是自找麻烦, \(p-1\) 而不是之前的 \(2\), 使得 \((9)\) 的最右边不能任意小. 为此, 现在需要挑选 \(p\), 使得 \(\Omega(p-1)\) 可以任意大. 换句话说, 我们需要建立
引理 8 对任何实数 \(r\), 存在质数 \(p\), 使得
\[\omega(p-1)\gt r.\]
引理 8 不容易, 有几种途径可以避免 Dirichlet’s Theorem on Arithmetic Progressions. 这里的证明需要下面这个简单的
引理 9 \(p\) 为质数, \(a, b, \alpha,\beta, n\in\Bbb Z, \alpha,\beta\geqslant0, n>0, p\nmid ab, p^\alpha\| (a-b)\). 如果在 \(p=2\) 时, \(\alpha\geqslant2\); 在 \(p\geqslant3\) 时, \(\alpha\geqslant1\), 那么, \(p^\beta\| n\) 为真当且仅当 \(p^{\alpha+\beta}\|(a^n-b^n)\) 成立.
引理 8 的证明 设 \(n\) 是任意的正整数. 取 \(n\) 个质数 \(q_1\), \(q_2\), \(\dotsc\), \(q_n\), 并且 \(2^n\lt q_1\lt q_2\lt\dotsb\lt q_n\).
记 \(u=q_1q_2\dotsm q_n\), 设 \(x\) 为大于 \(u\) 的正偶数. 下面来证明: \(x^u-1\) 至少有一质因子 \(p\), 使得对任一 \(u\) 之真因子 \(d\), \(p\nmid(x^d-1)\).
若不然, 对 \(x^u-1\) 的任一质因子 \(p\), 存在 \(u\) 的真因子 \(d\), 使得 \(p\mid(x^d-1)\). 据引理 9, 有
\[v_p\left(x^u-1\right)\leqslant v_p\left(u(x^d-1)\right)\leqslant v_p\left(u\prod_{d|u, \,d\lt u}(x^d-1)\right).\]
故
\[\left(x^u-1\right)\big| u\prod_{d|u,\, d\lt u}\left(x^d-1\right).\]
另一方面, 因 \(2^n\lt q_1\), \(u\lt x\), 所以
\[u\prod_{d|u,\, d\lt u}\left(x^d-1\right)\lt u\prod_{d|u,\, d\lt u}x^d\lt ux^{d(u)q_2q_3\dotsm q_n}\lt x^{q_1q_2\dotsm q_n}-1=x^u-1,\]
这里 \(d(u)=2^n\) 表示 \(u\) 的正因子的个数. 这是不可能的!
现在, 设 \(x^u-1\) 的质因子 \(p\), 使得对任一 \(u\) 之真因子 \(d\), \(p\nmid(x^d-1)\). 也就是说,
\[\delta_p(x)=u.\]
注意 \(x^{p-1}\equiv1\pmod p\), 故而 \(u\mid (p-1)\), 即 \(q_1q_2\dotsm q_n\mid (p-1)\). 这表明 \(\omega(p-1)\geqslant n\).
注意, 对于 \((p-1)^{p_1p_2\dotsm p_m}+1\), 有一个类似引理 6 的结论, 这样我们可以避开引理 8:
引理 10 设质数 \(q\), 使得 \(q\mid ((p-1)^{p_1p_2\dotsm p_m}+1)\), 那么 \(q\geqslant p\), 并且
- \(v_p((p-1)^{p_1p_2\dotsm p_m}+1)=1\) ;
- 若 \(q\gt p\), 则 \(q\geqslant p_1\).
5. 符合要求的最小正整数是 \(69\).
先给个例子说明 \(k\geqslant69\).
令 \(f\colon X\to X\) 由
\[f(3i-2)=3i-1, f(3i-1)=3i, f(3i)=3i-2,\]
\(i=1\), \(2\), \(\dotsc\), \(30\); \(f(91)=f(92)=f(93)=\dotsb=f(99)=100\), \(f(100)=99\) 给定.
首先, 这个 \(f\) 满足问题的两个条件:
对任意 \(x\in X\), 显而易见 \(f(x)\ne x\);
记 \(B_i=\{3i-2, 3i-1, 3i\}\), \(i=1\), \(2\), \(\dotsc\), \(30\); \(B_{31}=\{99,100\}\), \(B_{32}=\{91,92,93,94,95,96,97,98\}\). 显然, \(\{B_1, B_2, \dotsc, B_{32}\}\) 是 \(X\) 的一个划分.
设 \(A\) 是 \(X\) 的一个\(40\) 元子集. 因 \(|B_{32}|=8\), 故
\[\sum_{i=1}^{31}|A\cap B_i|\geqslant40-8=32.\]
于是, 必有某个 \(i\)(\(1\leqslant i\leqslant31\)), 使得 \(|A\cap B_i|\geqslant2\). 设 \(a\), \(b\) 是此 \(A\cap B_i\) 的两个元素, 则 \(f(a)=b\) 与 \(f(b)=a\) 至少有一个成立. 从而, \(b\) 与 \(a\) 必至少有一个属于 \(f(A\cap B_i)\). 因之, \((A\cap B_i)\cap f(A\cap B_i)\), 更有 \(A\cap f(A)\), 不空.
现在, 我们指出: 如果 \(X\) 的子集 \(B\), 使得 \(B\cup f(B)=X\), 那么 \(B\) 的元素个数不能少于 \(69\).
事实上, \(B_{32}\cap f(B)=\varnothing\) 导出 \(B_{32}\subseteq B\).
对任意一个 \(B_i\)(\(i=1\), \(2\), \(\dotsc\), \(30\)), 从 \(B_i\subseteq B\cup f(B)\), 得
\[\left(B\cap B_i\right)\cup\left(f(B)\cap B_i\right)=B_i.\]
从而, \(\left|B\cap B_i\right|+\left|f(B)\cap B_i\right|\geqslant\left|B_i\right|=3\). 此时, \(\left|B\cap B_i\right|\), \(\left|f(B)\cap B_i\right|\) 必有一个 \(\geqslant2\). 注意, 若 \(x\in X\), 使得 \(f(x)\in B_i\), 则 \(x\in B_i\). 于是, 若 \(\left|f(B)\cap B_i\right|\geqslant2\), 那么 \(\left|B\cap B_i\right|\geqslant2\). 总而言之, \(B\cap B_i\) 的元素个数不少于 \(2\).
因为 \(B_{31}\subseteq B\cup f(B)\), 因此 \(99\in B\cup f(B)\). 若 \(99\in f(B)\), 则 \(100\in B\). 总之, \(B\cap B_{31}\) 的元素个数不少于 \(1\).
综合起来, \(B\) 的元素个数不少于 \(8+2\cdot30+1=69\).
下面来证明, 对任意满足条件的函数 \(f\), 都存在 \(X\) 的 \(69\) 元子集 \(B\), 使得 \(B\cup f(B)=X\).
\(A\) 是 \(X\) 的 \(40\) 元子集, 有 \(A\cap f(A)\ne\varnothing\). 换句话说, 必有 \(a\in A\), 使得 \(f(a)\in A\). 于是, 对 \(X\) 的任意 \(40\) 元子集 \(A_1\), 可选出 \(a_1\), \(b_1\in A_1\), 使得
\[f(a_1)=b_1.\]
类似地, 设 \(A_2\) 是 \(X\) 的满足 \(A_2\supseteq A_1\setminus\{a_1, b_1\}\) 的另一个的 \(40\) 元子集, 我们可选出 \(a_2\), \(b_2\in A_2\), 使得
\[f(a_2)=b_2.\]
这个过程, 重复进行, 一共 \(31\) 次. 至此, 我们得到了
\[f(a_i)=b_i, i=1,2,\dotsc,31,\]
并且 \(a_1\), \(b_1\), \(a_2\), \(b_2\), \(\dotsc\), \(a_{31}\), \(b_{31}\) 是 \(X\) 的 \(62\) 个互不相同的元素.
令
\[B=X\setminus\{b_1, b_2,\dotsc,b_{31}\},\]
此 \(B\) 有 \(69\) 个元素, 并且使得 \(B\cup f(B)=X\) 为真.
6. 记
\[A=\{a_1, a_2, \dotsc, a_k\}, B=\{b_1, b_2, \dotsc, b_l\}.\]
于是 \(n-1\geqslant a_i-b_j\geqslant1-n\), 其中 \(1\leqslant i\leqslant k\), \(1\leqslant j\leqslant l\).
令
\[S_m=\{a_i+b_j|a_i-b_j=m,a_i\in A, b_j\in B\}, \]
这里 \(m=1-n,2-n,3-n,\dotsc,n-2,n-1\). 注意, \((a_i, b_j)\ne(a_{i^\prime},b_{j^\prime})\), \(a_i-b_j=a_{i^\prime}-b_{j^\prime}\) 给出 \(a_i+b_j\ne a_{i^\prime}+b_{j^\prime}\), 因此
\[\sum_{m=1-n}^{n-1}|S_m|=|A|\cdot|B|.\]
于是, 必有某个 \(m\)(\(n-1\geqslant m\geqslant1-n\)), 使得
\[|S_m|\geqslant\frac{|A|\cdot|B|}{2n-1}.\]
任取 \(s\in S_m+S_m\), 记 \(s=(a_i+ b_j)+(a_{i^\prime}+b_{j^\prime})\), 这里 \(a_i- b_j=a_{i^\prime}-b_{j^\prime}=m\), 并且 \(a_i\), \(a_{j^\prime}\in A\), \(b_i\), \(b_{j^\prime}\in B\). 由此, 我们有
\[s=(a_i+ b_j)+(a_{i^\prime}+b_{j^\prime})=(a_i+(a_i-m))+((b_{j^\prime}+m)+b_{j^\prime})=2(a_i+b_{j^\prime}).\]
这样便验证了
\[S_m+S_m\subseteq2(A+B).\]
综上所述, 若把这个 \(S_m\) 取作 \(D\), 此 \(D\) 符合我们的要求.