2016 第 57 届 IMO 解答
Problem 1 (The Kingdom Of Belgium)
IMO 2016 Problem 1
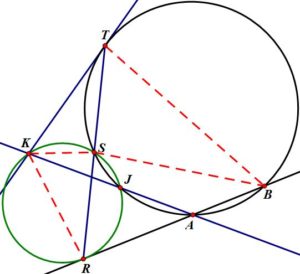
注意 \(\triangle FAB\), \(\triangle DAC\), \(\triangle EAD\) 是顶角相等的等腰三角形, 即
\[\angle FBA=\angle FAB=\angle DAC=\angle DCA= \angle EAD=\angle EDA.\]
既然 \(\triangle FAB\sim \triangle DAC\), 于是 \(\triangle ABC\sim \triangle AFD\), 进而
\begin{equation}\begin{split}\angle FDC&=180^\circ-\angle ADF-\angle DAC-\angle DCA\\&=180^\circ-\angle ACB-\angle FAB-\angle FBA\\&=\angle FBC=90^\circ,\end{split}\end{equation}
\(D\) 落在以 \(M\) 为心, \(MB\) 为半径的圆上, 即 \(D\), \(F\), \(B\), \(C\) 四点共圆, 并且 \(FC\) 即为此圆的直径. 记这个圆为 \(\Gamma_1\). 然后, \(\angle FBD=\angle FCD=\angle FBA\) 表明 \(FB\) 平分 \(\angle DBA\). 结合 \(AF\) 是 \(\angle DAB\) 的平分线, 我们知道 \(F\) 就是 \(\triangle DAB\) 的内心, 并且 \(DA=DB\), 这是因为
\[\angle DBA=2\angle FBA=\angle DAB.\]
从 \(\angle DBA+\angle DEA =2\angle FAB+\angle DEA=180^\circ\) 得出 \(E\), \(A\), \(B\), \(D\) 四点共圆. \(EA=ED\), 以及 \(F\) 为 \(\triangle DAB\) 的内心蕴涵 \(E\), \(F\), \(B\) 三点共线, \(EF=EA=ED\).
\(M\) 是直角三角形 \(FBC\) 的斜边 \(FC\) 的中点, 因此 \(MF=MB\). 由
\[\angle MFB= \angle FBA+\angle FBA=\angle DAB\]
得出 \(\triangle MFB\sim \triangle DAB\), 进而 \(\angle FMB=\angle ADB\), 于是 \(M\), \(D\), \(A\), \(B\) 四点共圆. 至此, 我们已经明白, \(A\), \(B\), \(M\), \(D\), \(E\) 五点共圆 \(\Gamma_2\). \(\angle ADE=\angle EAD=\angle DAC=\angle BAM\) 说明 \(AE=ED=MD=MB\).
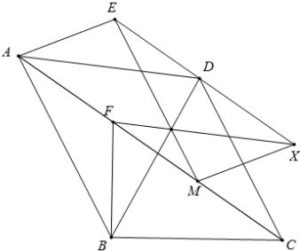
四边形 \(MXEA\) 为平行四边形, \(MX=AE=MB\) 定出 \(X\) 位于以 \(M\) 为心, \(MB\) 为半径的圆上, 即 \(D\), \(F\), \(B\), \(C\), \(X\) 五点共圆
由
\[\angle DEA+\angle EAC= \angle DEA+(\angle EAD+\angle DAC)=\angle DEA+(\angle EAD+\angle EDA)=180^\circ\]
蕴涵 \(ED\parallel AC\). 既然 \(EX\parallel AC\), 从而 \(E\), \(D\), \(X\) 三点共线.
既然 \(MX=AE=FE\), \(FM\parallel EX\), 从而四边形 \(FMXE\) 为等腰梯形, 四边形 \(FMXE\) 在圆 \(\Gamma_3\) 上.
最后, \(\Gamma_1\), \(\Gamma_2\), \(\Gamma_3\) 两两的根轴 \(BD\), \(FX\), \(ME\) 是相交于同一点.
解答二
Problem 2 ( Australia)
先来指出符合要求的 \(n\) 必须 \(9\mid n\).
事实上, 如果在一张 \(n \times n\) 方格表填入字母 \(I\), \(M\), \(O\) 满足要求, 显然 \(3\mid n\). 令 \(n=3k\), 这里 \(k\) 是正整数. 我们来考察符合下列三个条件之一的所有格子:
- 第一类: 第 \(2\), \(5\), \(8\), \(\dotsc\), \(3k-1\) 行的所有格子;
- 第二类: 第 \(2\), \(5\), \(8\), \(\dotsc\), \(3k-1\) 列的所有格子; 以及
- 第三类: 小方格个数是三的倍数的所有对角线上的全部格子.
注意, 这个\(n \times n\) 方格表中既属于第一类也属于第二类的格子对我们考察的格子的贡献为 \(4\) 次, 而这个方格表其余的格子对我们考察的格子的贡献恰是 \(1\) 次. 由此, 这个\(n \times n\) 方格表中既属于第一类也属于第二类的格子, 也就是这个方格表的第 \(2\), \(5\), \(8\), \(\dotsc\), \(3k-1\) 行; 第 \(2\), \(5\), \(8\), \(\dotsc\), \(3k-1\) 列的交叉处的全部 \(k^2\) 个格子恰有三分之一填入字母 \(I\), 三分之一填入字母 \(M\), 三分之一填入字母 \(O\). 这就迫使 \(3\mid k^2\), 进而 \(3\mid k\). 现在我们清楚 \(9 \mid n\).
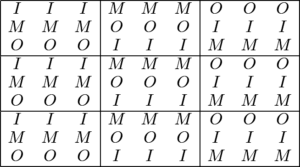
现在, 我们说明当 \(9 \mid n\) 之时, 可在一张 \(n \times n\) 方格表填入字母 \(I\), \(M\), \(O\) 满足要求.
当 \(n=9\) 时的构造如下:
IMO 2016 Problem 2 Proof 1
对于 \(n=9l\) (\(l\) 是正整数), 取 \(l^2\) 个这样的已经填入字母 \(I\), \(M\), \(O\) 的 \(9 \times 9\) 方格表. 然后, 按照每行 \(l\) 个, 每列 \(l\) 个这样的 \(9 \times 9\) 方格表排成一个 \(n \times n\) 的方格表.
对这个 \(l\times l\) 方格表, 其每一行(列)是如上的 \(9 \times 9\) 方格表的某一行(列)重复 \(l\) 次, 因此, 这个\(l\times l\) 方格表, 其每一行(列)有同样数目的字母 \(I\), \(M\), \(O\).
这个 \(l\times l\) 方格表的任一条数目是三的倍数的对角线穿过了一些 \(9 \times 9\) 方格表. 既然小方格 \((i,j)\) 在有三的倍数个数的小方格的某条对角线上, 当且仅当 \(i\equiv j\pmod 3\) 或 \(i+j\equiv 1\pmod 3\), 于是此 \(l\times l\) 方格表的对角线在这样的一个 \(9 \times 9\) 方格表内的部分恰是这 \(9 \times 9\) 方格表的一条数目是三的倍数的对角线, 因此这部分, 进而这个 \(l\times l\) 方格表的任一条数目是三的倍数的对角线, 有同样数目的字母 \(I\), \(M\), \(O\).
综上所述, 我们寻找的所有符合要求的正整数 \(n\) 恰是 \(9\) 的倍数的全体正整数.
Problem 3 ( Russia)
这是本届赛事最难的题, 只有 10 份考卷写出了正确的答案.
这个题的路途是有多种工具, 尤其如果允许稍微一点点的代数数论.
结果可以稍微加强:
设圆内接多边形 \(P=A_1A_2\dotsm A_k\) 的面积为 \(S\), 且对于任意三角形 \(A_iA_jA_l\)(\(1\leqslant i\lt j\lt l\leqslant k\)), 其面积 \(S_{\triangle A_iA_jA_l}\) 满足 \(2S_{\triangle A_iA_jA_l}\) 是正整数. 设 \(n\) 是一个正奇数, 满足 \(P\) 的每条边的长度的平方是被 \(n\) 整除的正整数, 且 \(P\) 的每条对角线长度的平方是正整数. 那么, \(2S\) 是正整数, 且被 \(n\) 整除.
只要指出, 对于 \(n=p^\alpha\), 结论为真即可(\(p\) 为奇质数, \(\alpha\) 是正整数).
对 \( k\) 进行归纳.
在 \( k=3\) 的时刻, 记 \(P\) 的边长为 \(a\), \(b\), \(c\). 根据 \(n\mid(a^2, b^2, c^2)\) 以及
\[16S^2=2a^2b^2+2b^2c^2+2c^2a^2-a^4-b^4-c^4\]
得 \(n^2\mid 16S^2\), 也就是 \(n^2\mid (4S)^2\). 于是 \(n\mid 4S\), 进而 \(n\mid 2S\).
假定当 \(k\) 是满足 \(3\leqslant k\lt m\) 时 (\(m\geqslant4\) 是正整数), \(n\mid 2S\). 我们来考察 \(k=m\).
设
\[A_iA_j^2=p^{\alpha_{ij}}z_{ij},\;\alpha_{ij}\in\Bbb N,\; z_{ij}\in\Bbb N, \;\big(z_{ij}, p\big)=1, \; 1\leqslant i\lt j\leqslant m,\]
这里 \(\Bbb N\) 为全部非负整数组成的集合. 于是, 当 \(j=i+1\) 时, \(\alpha_{ij}\geqslant \alpha\). 这里, 我们认为 \(A_{m+1}=A_1\).
设
\[u=\max\{\alpha_{ij}, \; 1\leqslant i\lt j\leqslant m,\; j-i\gt1\}.\]
我们指出, 必有 \(u\geqslant \alpha\).
如若不然, \(0\leqslant u\lt \alpha\). 记 \(v=\min\{\alpha_{ij}, \; 1\leqslant i\lt j\leqslant m,\; j-i\gt1\}\). 选择两个符合 \(1\leqslant i\lt j\leqslant m\), \(j-i\gt1\) 的正整数 \(i\), \(j\), 使得 \(p^v\parallel A_iA_j^2\). 观察四边形 \(A_{i-1}A_iA_{i+1}A_j\)(约定 \(A_0=A_m\)):
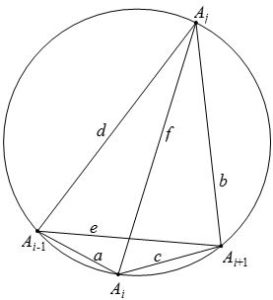
IMO 2016 Problem 3 Proof 1
Ptolemy 定理给出
\[ab+cd=ef.\]
两端平方
\[a^2b^2+c^2d^2+2abcd=e^2f^2.\]
可见, \(2abcd\) 是正整数. 注意,
\[2abcd=2\sqrt{p^{\alpha_{(i-1)i}+\alpha_{(i+1)j}+\alpha_{i(i+1)}+\alpha_{(i-1)j}}z_{(i-1)i}z_{(i+1)j}z_{i(i+1)}z_{(i-1)j}}=2p^{\alpha+v}\sqrt z, \]
这里 \(z=p^{\alpha_{(i-1)i}+\alpha_{(i+1)j}+\alpha_{i(i+1)}+\alpha_{(i-1)j}-2\alpha-2v}z_{(i-1)i}z_{(i+1)j}z_{i(i+1)}z_{(i-1)j}\) 是正整数. 于是, 正整数的算术平方根 \(\sqrt z\) 是有理数, 进而, 是正整数. 从而 \(p^{\alpha+v}\mid 2abcd\).
显而易见, \(p^{\alpha+v}\mid a^2b^2\), \(p^{\alpha+v}\mid c^2d^2\) 蕴涵 \(p^{\alpha+v}\mid e^2f^2\). 这是不可能的: \(p^v\parallel f^2\), \(a_{(i-1)(i+1)}\lt\alpha\).
既然 \(u\geqslant \alpha\), 也就是说 \(P\) 的至少一条对角线长度的平方是被 \(p^\alpha\) 整除. 这对角线把 \(P\) 分为两个小的圆内接多边形 \(P_1\) 和 \(P_2\). 记 \(P_1\) 和 \(P_2\) 的面积分别 \(S_1\) 和 \(S_2\). 于是 \(p^\alpha\mid 2S_1\), \(p^\alpha\mid 2S_2\). 然后 \(p^\alpha\mid (2S_1+2S_2)\), 此即 \(p^\alpha\mid 2S\). 至此, 我们完成了理想.
Problem 4 (Luxembourg)
当 \(n\in\Bbb N\), 则
- \(\big(P(n),P(n+1)\big)=1\);
- \(\big(P(n),P(n+2)\big)\mid7;\;\big(P(n),P(n+2)\big)=7 \iff n\equiv 2\pmod 7\);
- \(\big(P(n),P(n+3)\big)\mid3;\;\big(P(n),P(n+3)\big)=3 \iff n \equiv 1 \pmod3\);
- \(\big(P(n),P(n+4)\big)\mid19;\;\big(P(n),P(n+4)\big) = 19 \iff n \equiv 7 \pmod{19}\).
选择正整数 \(a\), 使得
\[a \equiv 7\pmod{19},\; a+1 \equiv 2\pmod7,\; a+2 \equiv 1\pmod 3,\]
这样的 \(a\) 可以
\[\big(P(a),P(a+4)\big)=19,\; \big(P(a+1),P(a+3)\big)=7,\; \big(P(a+2),P(a+5)\big)=3.\]
于是, \(b=6\) 符合要求.
事实 1 不仅表示 \(b\gt2\), 也说明 \(b=3\) 不可能: \(P(a+1)\), \(P(a+2)\), \(P(a+3)\) 中的 \(P(a+2)\) 与另外两个元素都互素.
\(P(a+1)\), \(P(a+2)\), \(P(a+3)\), \(P(a+4)\), 因为 \(\big(P(a+1),P(a+3)\big)=7\) 与 \(\big(P(a+2),P(a+4)\big)=7\) 不能同时成立, 故 \(b=4\) 不可能存在非负整数 \(a\) 满足要求.
对于 \(P(a+1)\), \(P(a+2)\), \(P(a+3)\), \(P(a+4)\), \(P(a+5)\), 由于 \(P(a+3)\) 与 \(P(a+2)\) 以及 \(P(a+4)\) 都互素, 如果 \(P(a+3)\) 与 \(P(a+1)\) 以及 \(P(a+5)\) 的一个不互素, 则必定 \(7\mid P(a+3)\), \(P(a+2)\) 以及 \(P(a+4)\) 都不是 \(7\) 的倍数, 进而 \(\big(P(a+2),P(a+4)\big)=1\). 注意
\[ \big(P(a+2),P(a+5)\big)=3,\; \big(P(a+1),P(a+4)\big)=3\]
不能同时为真, 因此 \(b=5\) 不可能存在非负整数 \(a\) 满足要求.
Lemma 1 当 \(n\) 为正整数, \(9\not\mid P(n) \).
事实上, 注意
\[4(n^2+n+1)=(2n+1)^2+3,\]
无论 \(3\mid (2n+1) \) 与否, 都有 \(9\not\mid \big((2n+1)^2+3\big) \). 因此, \(9\not\mid P(n) \).
Lemma 2 当 \(n\), \(m\) 都是正整数, \(\big(P(n),P(n+m)\big)\mid (m^3+3m)\).
首先, \(P(n+m)-P(n)=m^2+2nm+m\), 以及
\begin{equation}\begin{split}n\big(P(n+m)-P(n)\big)-2mP(n)&=\big(2mn^2+(m^2+m)n\big)-\big(2mn^2+2mn+2m\big)\\&=\big(m^2-m\big)n-2m.\end{split}\end{equation}
于是 \(\big(P(n),P(n+m)\big)\mid \big(X, Y\big)\), 这里 \(X=m^2+2nm+m\), \(Y=\big(m^2-m\big)n-2m\). 然后
\[\big(m-1\big)X-2Y=\big(m-1\big)(m^2+2nm+m)-2\Big(\big(m^2-m\big)n-2m\Big)=m^3+3m.\]
Lemma 3 命 \(p\) 为素数. 同余方程
\[x^2+a_1x+a_0\equiv 0\pmod p\]
之解数 \(\leqslant 2\).
Lemma 4 当整数 \(t \equiv n, n^2\pmod{P(n)}\), 必定 \(P(t) \equiv 0 \pmod{P(n)}\).
事实上, 在 \(t \equiv n^2 \pmod {P(n)}\) 时,
\[P(t)\equiv n^4 + n^2 + 1 = (n^2-n+1) (n^2+n+1) \equiv 0 \pmod {P(n)}.\]
于是,
\(n \equiv 1 \pmod 3\), 则 \(P(n) \equiv 0 \pmod 3\);
\(n \equiv 2,4 \pmod 7\), 则 \( P(n)\equiv 0 \pmod 7\);
\(n\equiv7, 49\pmod{57}\), 则 \( P(n)\equiv 0\pmod {57}\). 这导致当 \(n\equiv 7, 11\pmod {19}\) 时, 有 \(P(n)\equiv0\pmod{19}\)
至此, 结合 Lemma 3, 并且注意 \(n \equiv 0, 2 \pmod 3\) 蕴涵 \(3\not\mid P(n) \), 以及 Leamma 1, 2 揭示 \(\big(P(n),P(n+1)\big)=1\), \(\big(P(n),P(n+2)\big)\mid7\),\(\big(P(n),P(n+3)\big)\mid3\), \(\big(P(n),P(n+4)\big)\mid19\). 断言事实 1, 2, 3, 4 为真.
Problem 5 ( Russia)
既然 \(x-1\), \(x-2\), \(\dotsc\), \(x-2016\) 都在方程两边恰出现一次, 因此, 欲使得到的方程无实数解, 这 \(2016\) 个一次因式中的每个至多只能在两边出现一次, 即等号两边要擦去至少这 \(2016\) 个一次因式各一次. 故此, \(k\geqslant2016\).
下面我们来指出: 擦去左边所有形如 \(x-(4t-2)\), \(x-(4t-1)\), 右边所有形如 \(x-4t\), \(x-(4t-3)\)(即 \(t=1\), \(2\), \(\dotsc\), \(504\)) 的因式后, 得到的方程
\begin{equation}\begin{split}&\hspace3.25ex(x-1)(x-4)(x-5)(x-8)\dotsm(x-2013)(x-2016)\\&=(x-2)(x-3)(x-6)(x-7)\dotsm(x-2014)(x-2015)\end{split}\end{equation}
无实数根.
事实上, 注意下列 \(504\) 个不等式都是对任意实数 \(x\) 为真:
\begin{equation}\begin{split}
(x-1)(x-4)&\lt(x-2)(x-3);\\
(x-5)(x-8)&\lt(x-6)(x-7);\\
&\vdots\\
(x-2013)(x-2016)&\lt(x-2014)(x-2015).\end{split}\end{equation}
当 \(x\lt1\), \(x\gt2016\), 或存在正整数 \(m\)(\(1\leqslant m\leqslant503\)), 使得 \(4m\lt x\lt4m+1\), 这三种情况之一为真, 上面的 \(504\) 个不等式的两边都为正, 当然 \(x\) 不是方程 \((3)\) 的实数根; 当 \(x\in\{1, 2, 3, \dotsc, 2016\}\) 之时, \((3)\) 的一边为 \(0\), 一边非 \(0\), 因此 \(x\) 不是实数根; 当存在正整数 \(n\)(\(1\leqslant n\leqslant504\)), 使得 \(4n-3\lt x\lt4n-2\) 或 \(4n-1\lt x\lt4n\), 上面的第 \(n\) 个不等式的左边为负, 右边为正, 其余的 \(503\) 个不等式的两边都为正, 因此 \(x\) 不是方程 \((3)\) 的实数根.
剩下的任务, 是解释当 \(x\) 满足 \(4n-2\lt x\lt4n-1\)(\(n\) 是符合 \(1\leqslant n\leqslant504\) 的正整数)时, \(x\) 依旧不是方程 \((3)\) 的根.
注意到下列 \(503\) 个不等式都是对任意实数 \(x\) 为真:
\begin{equation}\begin{split}
(x-4)(x-5)&\gt(x-3)(x-6);\\
(x-8)(x-9)&\gt(x-7)(x-10);\\
&\vdots\\
(x-2012)(x-2013)&\gt(x-2011)(x-2014).\end{split}\end{equation}
当 \(x\) 符合 \(2\leqslant 4n-2\lt x\lt4n-1\leqslant2015\)(\(1\leqslant n\leqslant504\)) 时, (\(5\)) 中的 \(503\) 个不等式的两边都为正, 并且
\[ x-1\gt x-2\gt0,\]
\[-(x-2016)\gt-(x-2015)\gt0.\]
进而, 我们发现
\begin{equation*}-(x-1)(x-4)(x-5)(x-8)\dotsm(x-2013)(x-2016)\gt-(x-2)(x-3)(x-6)(x-7)\dotsm(x-2014)(x-2015)\end{equation*}
因此, 满足 \(4n-2\lt x\lt4n-1\)(\(n\) 是符合 \(1\leqslant n\leqslant504\) 的正整数) 的 \(x\) 不是方程 \((3)\) 的根.
综合起来, 符合要求的正整数 \(k\) 的最小值为 \(2016\).
Problem 6 (The Czech Republic)
可以认为这 \(n\) 条线段是圆的 \(n\) 条弦, 这些弦两两在圆内相交, 任三条弦不交于同一点(否则, 取一个足够大的圆, 使得全部的 \(n\) 条线段都在圆内. 用这些线段所在的直线被这个圆所截的弦来代替这 \(n\) 条线段).
把这 \(n\) 条弦的所有端点依逆时针记为 \(P_1\), \(P_2\), \(\dotsc\), \(P_{2n}\)(下面, 当整数 \(x\), \(y\) 满足 \(x\equiv y\pmod{2n}\) 时, \(P_x\), \(P_y\) 是同一点).
注意, \(P_i\), \(P_{i+n}\) 是同一条弦的两个端点, \(i=1\), \(2\), \(\dotsc\), \(n\).
这是因为, 对于任意两条相交弦, 任意一条的两个端点一定不在另一条的同一侧. 于是, 对于这 \(n\) 条弦的任意一条, 其一侧恰有剩下的 \(n-1\) 条弦的每条弦的一个端点, 另一侧亦有其余的这 \(n-1\) 条弦的每条弦的一个端点. 从而, 任意一条弦的任一侧恰有剩下的 \(n-1\) 条弦的全部 \(2(n-1)\) 个端点中的 \(n-1\) 个, 即线段 \(P_iP_{i+n}\) 是这 \(n\) 条弦中之一.
(a) 在 \(n\) 为奇数, 把青蛙放在 \(P_1\), \(P_3\), \(\dotsc\), \(P_{2n-1}\), 可以实现他的愿望.
首先, 这 \(n\) 个点中的任意两个, 不可能是同一条弦的两个端点. 因为当且仅当整数 \(x\), \(y\) 满足 \(x\equiv y\pmod n\) 时, \(P_x\), \(P_y\) 是同一条弦的端点(包括重合). 在正整数 \(i\), \(j\in\{1, 3, 5, \dotsc, 2n-1\}\), \(i\ne j\), 必定 \(i-j\ne0\), \(-2n\lt i-j\lt2n\). \(i-j\) 是偶数, \(n\) 为奇数蕴涵 \(i-j\ne n\), \(-n\). 故而 \(i\not\equiv j\pmod n\), 即 \(P_i\), \(P_j\) 不是同一条弦的两个端点.
杰夫能实现他的愿意.
事实上, 记 \(P_i\), \(P_j\) 是 \(P_1\), \(P_3\), \(\dotsc\), \(P_{2n-1}\) 中的任意两点. 设弦 \(P_iP_{i+n}\) 与 \(P_jP_{j+n}\) 的交点为 \(A\).
\(P_i\), \(P_j\) 之间有奇数个点(不包括这两点本身). 这奇数个点组成集合 \(S\). 不以 \(S\) 中的点为端点的弦如果与线段 \(P_iA\), \(P_jA\) 中的一个相交, 则必定也与另一个相交, 因为此弦的端点不属于 \(S\), 即不能在\(P_i\), \(P_j\) 之间; 以 \(S\) 中的点为端点的弦必定与线段 \(P_iA\), \(P_jA\) 中的恰好一个相交. \(S\) 有奇数个点, 这表明线段 \(P_iA\), \(P_jA\) 与所有的 \(n\) 条弦的交点个数的奇偶性不同. 进而, 从 \(P_i\), \(P_j\) 出发的青蛙, 任何时刻都不会落在同一个交点.
(b) 杰夫想实现他的理想的话, 青蛙不能放在圆上相邻的端点.
事实上, 记 \(P_i\), \(P_{i+1}\) 是 \(P_1\), \(P_2\), \(\dotsc\), \(P_{2n}\) 中相邻的两点, 即 \(i\in\{1, 2, 3, \dotsc, 2n\}\). 设弦 \(P_iP_{i+n}\) 与 \(P_{i+1}P_{i+1+n}\) 的交点为 \(B\).
所有的 \(n\) 条弦的任意的一条, 如果与线段 \(P_iB\), \(P_{i+1}B\) 中的一个相交, 则必定也与另一个相交, 鉴于此弦的端点不能在\(P_i\), \(P_{i+1}\) 之间. 于是, 线段 \(P_iB\), \(P_{i+1}B\) 与所有的 \(n\) 条弦的交点个数相同. 进而, 从 \(P_i\), \(P_{i+1}\) 出发的青蛙, 会在某个时刻落在同一个交点.
既然青蛙不能放在圆上相邻的端点, 于是, 青蛙只能全部放在 \(P_1\), \(P_3\), \(\dotsc\), \(P_{2n-1}\) 或 \(P_2\), \(P_4\), \(\dotsc\), \(P_{2n}\). 记住 \(n\) 是偶数, 在前一种情况, \(P_1\), \(P_{n+1}\) 有青蛙; 在后一种情况, \(P_2\), \(P_{n+2}\) 有青蛙. 不幸的悲剧是, \(P_1\), \(P_{n+1}\) 或 \(P_2\), \(P_{n+2}\) 都是一条弦的两个端点.
Annotations
- 今年的题, 如果时间充裕一点, 应该都能做出来
- 又一次的证明, 出现精彩万分的数论题是多么不容易.
- 最好的题是第 3 题, 毫无疑问. 本题需要一点智慧. 如果知道一点代数数论, 本题是有好几种突破口, 请参看续集 IMO 2016 solutions II.
- 题 6 不适合作为 Q3 或 Q6, 难度不够, 似乎比 Q2 容易.